How to Prove a Set of Functions is Closed Under Addition (Example with functions s.t. f(0) = 0)

Closure Under Addition (Sets of Whole Numbers)

Determine whether a set is closed or open

Show the Set of Functions such that f(0) = 1 is Not Closed Under Addition

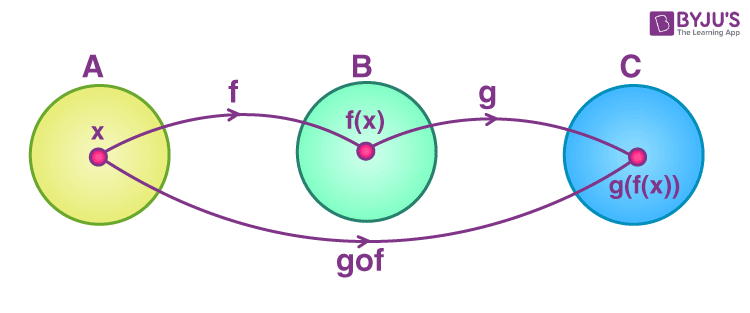
Composition of Functions - Definition, Properties and Examples

Solved Let F be the set of all real-valued functions with

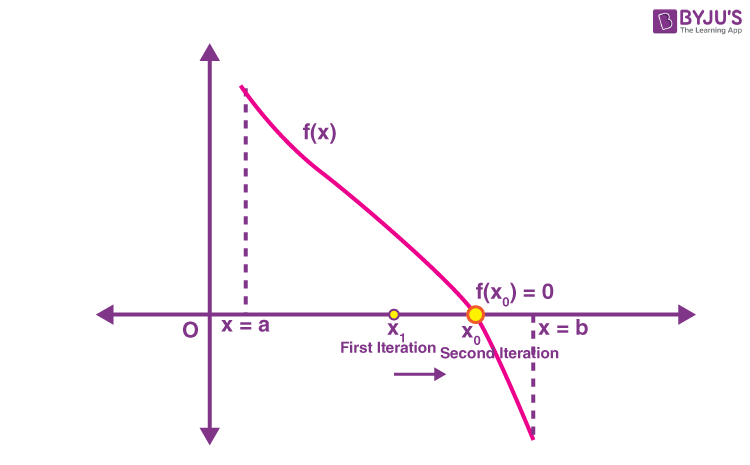
Bisection Method Questions (with Solutions)

SOLVED: 3. For the following relations, either prove it is an equivalence relation or give a counterexample and justify why it is not: (a) f Rg in F, the set of all

Types of Functions: Classification, One-One, Onto, and Examples

Solved Theory (Applying concepts to prove facts) 1. Prove

general topology - Topological spaces in which a set is the support of a continuous function iff it is the closure of a open set. - Mathematics Stack Exchange